

Star Wars Death Star illustration, Printed circuit board Electronic circuit, Earth Science and Technology Data, angle, electronics, sphere png 1376x1426px 551.52KB.Propeller Ship Motor Boats Archimedes' screw Drive shaft, props, transport, stock Photography, shaft png 600x540px 303.78KB.Brain Rules Principles of Neural Science Human brain Neuroimaging, Brain, people, human Brain, neuron png 902x916px 911.03KB.Archimedes' principle Buoyancy Fluid Force Spring scale, ppt sequence, angle, experiment, auto Part png 940x550px 79.98KB.Archimedes' screw Screw turbine Water turbine, screw, angle, technic, screw png 1529x1051px 538.09KB.Tver Invention International Innovation club "Archimedes" Technology, technology, electronics, food, innovation png 723x721px 374.19KB.Boat propeller Ship Archimedes' screw, Ship, Boat, propeller, Ship png 510x510px 165.58KB.As such, it is a more seminal argument than Archimedes’ “static” one, which does not provide much insight as to why the law is valid. The “kinetic” argument for the Law of the Lever given in the passage comes close to the idea of energy as the product of force and distance, to the concept of the conservation of energy, and to the principle of virtual velocities. It was probably written in the years between the death of Aristotle in 322 BC and the birth of Archimedes c. The above passage is from the Mechanica, a work believed to have been written by the Peripatetic School, which is the name given to the followers of Aristotle. Let AB be the bar, G be the weight, and D the moving force, E the fulcrum and let H be the point to which the moving force travels and K the point to which G the weight moved travels. The reason has been given before that the point further from the centre describes the greater circle, so that by the use of the same force, when the motive force is farther from the lever, it will cause a greater movement. Now the greater the distance from the fulcrum, the more easily it will move. For since under the impulse of the same weight the greater radius from the centre moves the more rapidly, and there are three elements in the lever, the fulcrum,that is the cord or centre, and the two weights, the one which causes the movement, and the one that is moved : now the ratio of the weight moved to the weight moving it is the inverse ratio of the distances from the centre. Is the lever the reason, being equivalent to a beam with a cord attached below, and divided into two equal parts? For the fulcrum acts as the attached cord : for both these remain stationary, and act as a centre.

Why is it that small forces can move great weights by means of a lever, as was said at the beginning of the treatise, seeing that one naturally adds the weight of the lever? For surely the smaller weight is easier to move, and it is smaller without the lever. Princeton University Press, Princeton, N.J., U.S.A., 1987 A discussion of these points can be found in pages 291-304 of the following book:īy E.J. While it is commonly stated that Archimedes proves this law in these two propositions, there has been considerable debate as to what Archimedes really proved, what his stated postulates mean, what hidden assumptions he used, and what he may have thought he proved. This is the statement of the Law of the Lever that Archimedes gives in Propositions 6 and 7 of Book I of his work entitled On the Equilibrium of Planes.

Magnitudes are in equilibrium at distances reciprocally proportional to their weights.
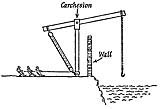
The Law of the Lever According to Archimedes.


 0 kommentar(er)
0 kommentar(er)
